ベイズの定理（Bayes' Theorem）とは？-AI関連の用語集【クラベルAI】-

ベイズの定理（Bayes' Theorem）

ベイズの定理（Bayes’ Theorem）は、ある事象が起こったあとにその原因や確率を見直す（更新する）ための統計的な考え方・公式です。

ベイズの定理の式は以下の通りです。

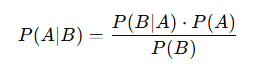
• P(A∣B)：Bが起こったときにAが起こっている確率（事後確率）

• P(B∣A)：Aが起こったときにBが起こる確率（尤度：ゆうど）

• P(A)：Aが起こるもともとの確率（事前確率）

• P(B)：Bが起こる全体の確率（正規化定数）

この定理は、新しい情報（B）が得られたときに、もともとの予測（Aの確率）をどう変えるかを教えてくれます。

医療、機械学習、自然言語処理、スパムフィルタ、意思決定など、さまざまな分野で使われています。

ベイズの定理（Bayes' Theorem）関連用語

ベイズの定理（Bayes' Theorem）に関連する単語は以下の通りです。

ベイズの定理（Bayes' Theorem）やさしい解説

ベイズの定理は、「何か新しいことがわかったときに、それをもとに予想を見直すための考え方」です。

例えば、こんな場面を考えてみてください。

• もともと、あなたが かぜをひいている可能性は 30％、花粉症の可能性は 70％ でした。
• でもある日、「くしゃみ」が出ました。
• 実は、「かぜの人がくしゃみをする確率」は50％、「花粉症の人がくしゃみをする確率」は90％です。

→ この新しい情報（くしゃみ）を手がかりに、「やっぱり花粉症の可能性が高いな」と予想を見直すのがベイズの定理の考え方です。

AI関連の用語集【まとめ】

AI関連の用語集が気になる方のために、用語集一覧を作成しました。AIに関する学びを深めたいとお考えの方はぜひご覧ください。